Coupled Oscillator: Coupled Mass-Spring System with Input

Setup State Space Equation

Problem Statement

Find an input function such that the lower mass, $m_{1}$, is stationary in the steady state. Find the equation of motion for the upper mass, $m_{2}$.

The use of one spring between the masses is just a simplification of a multi-spring system, so the possibility of being off-kilter is neglected and just the vertical forces are considered.

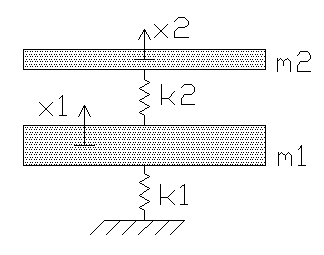
Initial Conditions and Values

$m_{1}=140kg{\frac {}{}}$

$k_{1}=108000{\frac {N}{m}}$

$m_{2}=80kg{\frac {}{}}$

$k_{2}=80000{\frac {N}{m}}$

Let the initial conditions be zero for the time being.

Force Equations

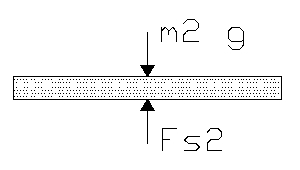
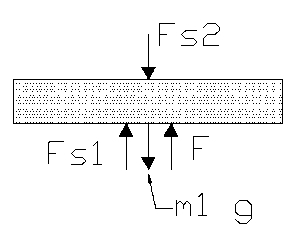
Sum of the forces in the x direction yields

For $m_{1}{\frac {}{}}$

$+\uparrow \sum F_{x_{2}}=m_{2}{\ddot {x}}_{2}$

$\Rightarrow \ m_{2}{\ddot {x}}_{2}=F_{s_{2}}-m_{2}g$

Since $F_{s_{2}}=k_{2}(L_{2}+x_{1}-x_{2})$

$\Rightarrow \ {\ddot {x}}_{2}=-g+{\frac {k_{2}}{m_{2}}}\,L_{2}+{\frac {k_{2}}{m_{2}}}\,x_{1}-{\frac {k_{2}}{m_{2}}}\,x_{2}$

And for $m_{1}{\frac {}{}}$

$+\uparrow \sum F_{x_{1}}=m_{1}{\ddot {x}}_{1}$

$\Rightarrow \ m_{1}{\ddot {x}}_{1}=F_{s_{1}}+F-m_{1}g-F_{s_{2}}$

Since $F_{s_{1}}=k_{1}(L_{1}-x_{1})$

Where $F{\frac {}{}}=F(t)$ is the input force

$\Rightarrow \ {\ddot {x}}_{1}=-g+{\frac {1}{m_{1}}}\,F+{\frac {k_{1}}{m_{1}}}\,L_{1}-{\frac {k_{1}}{m_{1}}}\,x_{1}-{\frac {k_{2}}{m_{1}}}\,L_{2}-{\frac {k_{2}}{m_{1}}}\,x_{1}+{\frac {k_{2}}{m_{1}}}\,x_{2}$

State Space Equation

The general form of the state equation is

${\underline {\dot {x}}}(t)={\widehat {A}}\,{\underline {x}}(t)+{\widehat {C}}\,{\underline {u}}(t)$

Where ${\widehat {M}}$ denotes a matrix and ${\underline {v}}$ denotes a vector.

Let $x_{1}{\frac {}{}}$, ${\dot {x}}_{1}{\frac {}{}}$, $x_{2}{\frac {}{}}$, and ${\dot {x_{2}}}{\frac {}{}}$ be the state variables, then

${\begin{bmatrix}{\dot {x}}_{1}\\{\ddot {x}}_{1}\\{\dot {x}}_{2}\\{\ddot {x}}_{2}\end{bmatrix}}=$ ${\begin{bmatrix}0&1&0&0\\{\frac {-k_{1}}{m_{1}}}&0&{\frac {k_{2}}{m_{1}}}&0\\0&0&0&1\\0&0&{\frac {-k_{2}}{m_{2}}}&0\end{bmatrix}}{\begin{bmatrix}x_{1}\\{\dot {x}}_{1}\\x_{2}\\{\dot {x}}_{2}\end{bmatrix}}+{\begin{bmatrix}0&0&0&0\\-1&{\frac {k_{1}}{m_{1}}}&{\frac {-k_{2}}{m_{1}}}&{\frac {1}{m_{1}}}\\0&0&0&0\\-1&0&{\frac {k_{2}}{m_{2}}}&0\end{bmatrix}}{\begin{bmatrix}g\\L_{1}\\L_{2}\\F\end{bmatrix}}$