Problem Statement

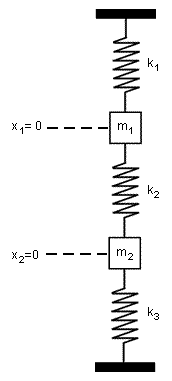
Derive the system of differential equations describing the straight-line vertical motion of the coupled spring shown in Figure 1. Use Laplace transform to solve the system when

k_{1} = k_{2} = k_{3} = 1

,

m_{1} = m_{2} = 1

, and

x_{1} (0) = 0

,

x^{'} 1 (0) = - 1

,

x_{2} (0) = 0

, and

x'_{2} (0) = 1

.

Solution

At positions $x_{1}$ and $x_{2}$ , the masses $m_{1}$ and $m_{2}$ are in equilibrium. Thus, the motion equations for $m_{1}$ and $m_{2}$ are,

 $m_{1} {\ddot{x}}_{1} = - k_{1} x_{1} + k_{2} (x_{2} - x_{1})$ 
∴  $m_{1} {\ddot{x}}_{1} + k_{1} x_{1} - k_{2} (x_{2} - x_{1}) = 0$

 $m_{2} {\ddot{x}}_{2} = - k_{2} (x_{2} - x_{1}) - k_{3} x_{2}$ 
∴  $m_{2} {\ddot{x}}_{2} + k_{2} (x_{2} - x_{1}) - k_{3} x_{2} = 0$

where $m_{1} x^{'}'_{1}$ and $m_{2} x^{'}'_{2}$ represent the Newton's Second Law of Motion and $- k_{1} x_{1} + k_{2} (x_{2} - x_{1})$ and $- k_{2} (x_{2} - x_{1}) - k_{3} x_{2}$ represent the net forces acting in the masses.

Laplace Transform

Applying the Laplace Transform to the motion equations and plugging the values of $k_{1}$ , $k_{2}$ , $k_{3}$ , $m_{1}$ , $m_{2}$ , $x_{1} (0)$ , $x^{'} 1 (0)$ , $x_{2} (0)$ , and $x'_{2} (0)$ for this systems, we obtain,

 $ℒ [m_{1} {\ddot{x}}_{1} + k_{1} x_{1} - k_{2} (x_{2} - x_{1})] = 0$ 

 $m_{1} [s^{2} X_{1} (s) - s x_{1} (0) - {\dot{x}}_{1} (0)] + k_{1} X_{1} (s) - k_{2} (X_{2} (s) - X_{1} (s)) = 0$ 
 
 $X_{1} (s) (m_{1} s^{2} + k_{1} + k_{2}) = m_{1} (s x_{1} (0) - {\dot{x}}_{1} (0)) + k_{2} X_{2} (s)$ 

 $X_{1} (s) = \frac{m_{1} (s x_{1} (0) + {\dot{x}}_{1} (0)) + k_{2} X_{2} (s)}{(m_{1} s^{2} + k_{1} + k_{2})}$ 

 $X_{1} (s) = \frac{1 (s 0 + (- 1)] + 1 X_{2} (s)}{(1 s^{2} + 1 + 1)}$ 

 $X_{1} (s) = \frac{X_{2} (s) - 1}{(s^{2} + 2)}$ 


 $ℒ [m_{2} {\ddot{x}}_{2} + k_{2} (x_{2} - x_{1}) + k_{3} x_{2}] = 0$ 

 $m_{2} [s^{2} X_{2} (s) - s x_{2} (0) - {\dot{x}}_{2} (0)] + k_{2} (X_{2} (s) - X_{1} (s)) + k_{3} X_{2} (s) = 0$ 

 $X_{2} (s) (m_{2} s^{2} + k_{2} + k_{3}) = m_{2} (s x_{2} (0) - {\dot{x}}_{2} (0)) + k_{2} X_{1} (s)$ 

 $X_{2} (s) = \frac{m_{2} (s x_{2} (0) + {\dot{x}}_{2} (0)) + k_{2} X_{1} (s)}{(m_{2} s^{2} + k_{2} + k_{3})}$ 

 $X_{2} (s) = \frac{1 (s 0 + 1) + 1 X_{1} (s)}{(1 s^{2} + 1 + 1)}$ 

 $X_{2} (s) = \frac{X_{1} (s) + 1}{(s^{2} + 2)}$

Finally, solving for $X_{1} (s)$ and $X_{2} (s)$ yields,

 $X_{1} (s) = \frac{- 1}{s^{2} + 3}$ 

 $X_{2} (s) = \frac{1}{s^{2} + 3}$

Inverse Laplace Transform

First, we recognize that

$s i n (k t) = ℒ^{- 1} {\frac{k}{s^{2} + k^{2}}}$

On the other hand, we identify that $k^{2} = 3$ , and so $k = \sqrt{3}$ . Hence, we fix the expression by multiplying and dividing by $\sqrt{3}$ ,

 $ℒ^{- 1} [X_{1} (s)] = ℒ^{- 1} [\frac{- 1}{s^{2} + 3}] = - \frac{1}{\sqrt{3}} ℒ^{- 1} [\frac{\sqrt{3}}{s^{2} + 3}] = - \frac{1}{\sqrt{3}} s i n (\sqrt{3} t)$ 

 $ℒ^{- 1} [X_{2} (s)] = ℒ^{- 1} [\frac{1}{s^{2} + 3}] = \frac{1}{\sqrt{3}} ℒ^{- 1} [\frac{\sqrt{3}}{s^{2} + 3}] = \frac{1}{\sqrt{3}} s i n (\sqrt{3} t)$

Laplace Transforms: Vertical Motion of a Coupled Spring System

Contents

Problem Statement

Solution

Laplace Transform

Inverse Laplace Transform

Navigation menu

Laplace Transforms: Vertical Motion of a Coupled Spring System

Problem Statement

Solution

Laplace Transform

Inverse Laplace Transform

Navigation menu

Search