Laplace Transforms: Vertical Motion of a Coupled Spring System

By Jimmy Apablaza

This problem is described in Exercise 14, Section 7.6 (page 323) of the A first Course in Differential Equations textbook, 8ED (ISBN 0-534-41878-3).

Figure 1. Coupled Spring System.

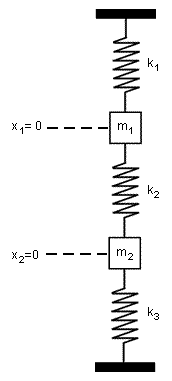
Problem Statement

Derive the system of differential equations describing the straight-line vertical motion of the coupled spring shown in Figure 1. Use Laplace transform to solve the system when $k_1=k_2=k_3=1\frac{}{}$, $m_1=m_2=1\frac{}{}$, and $x_1(0)=0\frac{}{}$, $x^{\prime }1(0)=-1\frac{}{}$, $x_2(0)=0\frac{}{}$, and $x{\text{'}}_2(0)=1\frac{}{}$.

Solution

At positions $x_1\frac{}{}$ and $x_2\frac{}{}$, the masses $m_1\frac{}{}$ and $m_2\frac{}{}$ are in equilibrium. Thus, the motion equations for $m_1\frac{}{}$ and $m_2\frac{}{}$ are,

$m_1{\ddot{x}}_1=-k_1{x}_1+k_2(x_2-x_1)$

∴$m_1{\ddot{x}}_1+k_1{x}_1-k_2(x_2-x_1)=0$

$m_2{\ddot{x}}_2=-k_2(x_2-x_1)-k_3{x}_2$

∴ $m_2{\ddot{x}}_2+k_2(x_2-x_1)-k_3{x}_2=0$

where $m_1{x}^{\prime }{\text{'}}_1\frac{}{}$ and $m_2{x}^{\prime }{\text{'}}_2\frac{}{}$ represent the Newton's Second Law of Motion and $-k_1{x}_1+k_2(x_2-x_1)\frac{}{}$ and $-k_2(x_2-x_1)-k_3{x}_2\frac{}{}$ represent the net forces acting in the masses.

Laplace Transform

Applying the Laplace Transform to the motion equations and plugging the values of $k_1\frac{}{}$, $k_2\frac{}{}$, $k_3\frac{}{}$, $m_1\frac{}{}$, $m_2\frac{}{}$, $x_1(0)\frac{}{}$, $x^{\prime }1(0)\frac{}{}$, $x_2(0)\frac{}{}$, and $x{\text{'}}_2(0)\frac{}{}$ for this systems, we obtain,

${ℒ}[m_1{\ddot{x}}_1+k_1{x}_1-k_2(x_2-x_1)]=m_1[s^2{X}_1(s)-s{x}_1(0)-{\dot{x}}_1(0)]+k_1{X}_1(s)-k_2(X_2(s)-X_1(s))=0$

$X_1(s)(m_1{s}^2+k_1+k_2)=m_1(s{x}_1(0)-{\dot{x}}_1(0))+k_2{X}_2(s)$

$X_1(s)=\frac{m_1(s{x}_1(0)+{\dot{x}}_1(0))+k_2{X}_2(s)}{(m_1{s}^2+k_1+k_2)}$

$X_1(s)=\frac{1(s0+(-1)]+1X_2(s)}{(1s^2+1+1)}$

$X_1(s)=\frac{X_2(s)-1}{(s^2+2)}$

${ℒ}[m_2{\ddot{x}}_2+k_2(x_2-x_1)+k_3{x}_2]=m_2[s^2{X}_2(s)-s{x}_2(0)-{\dot{x}}_2(0)]+k_2(X_2(s)-X_1(s))+k_3{X}_2(s)=0$

$X_2(s)(m_2{s}^2+k_2+k_3)=m_2(s{x}_2(0)-{\dot{x}}_2(0))+k_2{X}_1(s)$

$X_2(s)=\frac{m_2(s{x}_2(0)+{\dot{x}}_2(0))+k_2{X}_1(s)}{(m_2{s}^2+k_2+k_3)}$

$X_2(s)=\frac{1(s0+1)+1X_1(s)}{(1s^2+1+1)}$

$X_2(s)=\frac{X_1(s)+1}{(s^2+2)}$

Finally, solving for $X_1(s)\frac{}{}$ and $X_2(s)\frac{}{}$ yields,

$X_1(s)=\frac{-1}{s^2+3}$

$X_2(s)=\frac{1}{s^2+3}$

Inverse Laplace Transform

Error creating thumbnail: File missing

Figure 2. Coupled Spring System Motion.

First, we recognize that

$sin(kt)={{ℒ}}^{-1}\left\{\frac{k}{s^2+k^2}\right\}$

On the other hand, we identify that $k^2=3$, and so $k=\sqrt{3}$. Hence, we fix the expression by multiplying and dividing by $\sqrt{3}$,

$x_1(t)={{ℒ}}^{-1}[X_1(s)]={{ℒ}}^{-1}\left[\frac{-1}{s^2+3}\right]=-\frac{1}{\sqrt{3}}{{ℒ}}^{-1}\left[\frac{\sqrt{3}}{s^2+3}\right]=-\frac{1}{\sqrt{3}}sin(\sqrt{3}t)$

$x_2=(t){{ℒ}}^{-1}[X_2(s)]={{ℒ}}^{-1}\left[\frac{1}{s^2+3}\right]=\frac{1}{\sqrt{3}}{{ℒ}}^{-1}\left[\frac{\sqrt{3}}{s^2+3}\right]=\frac{1}{\sqrt{3}}sin(\sqrt{3}t)$

A plot of the oscillatory motion is shown on Figure 2.

Initial-Value & Final-Value Theorem

The initial-value and final-value theorem can be useful the finding the behavior of a function at small and large times respectively. By definition, the Initial-Value Theorem is,

$\underset{s\to \mathrm{\infty }}{\lim }sX(s)=x(0)$

and the Final-Value Theorem is,

$\underset{s\to 0}{\lim }sX(s)=x(\mathrm{\infty })$

Thus, applying both theorems to our the Laplace Transforms,

$\underset{s\to \mathrm{\infty }}{\lim }s{X}_1(s)=\underset{s\to \mathrm{\infty }}{\lim }s\frac{-1}{s^2+3}=\underset{s\to \mathrm{\infty }}{\lim }\frac{-s}{s^2+3}=\frac{-\mathrm{\infty }}{{\mathrm{\infty }}^2+3}=0=x_1(0)$

$\underset{s\to 0}{\lim }s{X}_1(s)==\underset{s\to 0}{\lim }s\frac{1}{s^2+3}=\underset{s\to 0}{\lim }\frac{s}{s^2+3}=\frac{0}{0^2+3}=0=x_1(\mathrm{\infty })$

$\underset{s\to \mathrm{\infty }}{\lim }s{X}_2(s)=\underset{s\to \mathrm{\infty }}{\lim }s\frac{1}{s^2+3}=\underset{s\to \mathrm{\infty }}{\lim }\frac{s}{s^2+3}=\frac{\mathrm{\infty }}{{\mathrm{\infty }}^2+3}=0=x_2(0)$

$\underset{s\to 0}{\lim }s{X}_2(s)==\underset{s\to 0}{\lim }s\frac{1}{s^2+3}=\underset{s\to 0}{\lim }\frac{s}{s^2+3}=\frac{0}{0^2+3}=0=x_2(\mathrm{\infty })$

Bode Plot

Error creating thumbnail: File missing

Figure 3. Bode Diagram.

The Bode plot for the Transfer Functions

$H_1(s)=\frac{-1}{s^2+3}$

and

$H_2(s)=\frac{1}{s^2+3}$

can be easily done using a program like Octave or MATLAB. The code is displayed below. From Figure 3 we may notice that the Amplitude vs. Frequency plot for both functions overlaps. The peak amplitude occurs at $\sqrt{3}\approx 1.73\frac{}{}$ seconds, as well as the phase switching as shown in the Phase vs. Frequency plot.

h1=tf([-1],[1 0 3]); 
h2=tf([1],[1 0 3]); 
bode(h1,'b',h2,'-.r');
legend('H_1(s)','H_2(s)')
grid on;

Magnitude Frequency Response

Considering the Transfer Functions $H_1(s)\frac{}{}$ and $H_2(s)\frac{}{}$ described in the Bode Plot section, we notice that there are no values for the s-variable that make $H_1(s)\frac{}{}$ and $H_2(s)\frac{}{}$ equal zero.

From the Bode Plot, we notice that the break point occurs at ≈ 1.73 seconds, so the

Convolution

By definition, the convolution of two functions is,

$y(t)=f(t)*h(t)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(\tau )h(t-\tau )d\tau =\underset{\mathrm{\infty }}{\overset{-\mathrm{\infty }}{\int }}f(t-\tau )h(\tau )d\tau$

where $h_1\frac{}{}$ refers to the inverse Laplace Transform. Assuming that $\tau \frac{}{}$ is a dummy variable of integration, and $f(t)\frac{}{}$ is the impulse function $(f_1(t)=f_2(t)=\delta (t)\frac{}{})$, the convolution for our system is,

$y_1(t)=\underset{0}{\overset{t}{\int }}\delta (t-\tau )h_1(\tau )d\tau =-\frac{1}{\sqrt{3}}\underset{0}{\overset{t}{\int }}\delta (t-\tau )sin(\sqrt{3}\tau )d\tau ={[-\frac{1}{\sqrt{3}}sin(\sqrt{3}\tau )]}_{\tau =t}=-\frac{1}{\sqrt{3}}sin(\sqrt{3}t)$

$y_2(t)=\underset{0}{\overset{t}{\int }}\delta (t-\tau )h_2(\tau )d\tau =\frac{1}{\sqrt{3}}\underset{0}{\overset{t}{\int }}\delta (t-\tau )sin(\sqrt{3}\tau )d\tau ={[\frac{1}{\sqrt{3}}sin(\sqrt{3}\tau )]}_{\tau =t}=\frac{1}{\sqrt{3}}sin(\sqrt{3}t)$

which is the same solution yields by the inverse Laplace Transform

State Equation Model

By definition, the the state equation is stated as

$\underset{\_}{\dot{x}}=\hat{A}\underset{\_}{x}+\hat{B}\underset{\_}{u}$

Now, consider the motion equations described in the Solution section,

$m_1{\ddot{x}}_1+k_1{x}_1-k_2(x_2-x_1)=m_1{\ddot{x}}_1+k_1{x}_1-k_2{x}_2+k_2{x}_1=0$

$m_2{\ddot{x}}_2+k_2(x_2-x_1)-k_3{x}_2=m_2{\ddot{x}}_2+k_2{x}_2-k_2{x}_1-k_3{x}_2=0$

Solving for ${\ddot{x}}_1$ and ${\ddot{x}}_2$ yields,

${\ddot{x}}_1=-\frac{k_1}{m_1}{x}_1+\frac{k_2}{m_1}{x}_2-\frac{k_2}{m_1}{x}_1$

${\ddot{x}}_2=\frac{-k_2}{m_2}{x}_2+\frac{k_2}{m_2}{x}_1+\frac{k_3}{m_2}{x}_2$

Finally, we let $x_1\frac{}{}$, ${\dot{x}}_1\frac{}{}$, $x_2\frac{}{}$, and $\dot{x_2}\frac{}{}$ be the state variables. Thus,

$\left[\begin{array}{c}{\dot{x}}_1\\ {\ddot{x}}_1\\ {\dot{x}}_2\\ {\ddot{x}}_2\end{array}\right]=\left[\begin{array}{cccc}0& 1& 0& 0\\ -\frac{1}{m_1}(k_1+k_2)& 0& \frac{k_2}{m_1}& 0\\ 0& 0& 0& 1\\ \frac{k_2}{m_2}& 0& \frac{1}{m_2}(k_3-k_2)& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ {\dot{x}}_1\\ x_2\\ {\dot{x}}_2\end{array}\right]$