Derivative Matrix for a Function Vector

Author

John Hawkins

Problem

The following problem statement is that proposed by Prof. Frohne on the main class page:

1. Explore how a linear operator, like for example $\frac{d}{dt}$ can be represented as some kind of a matrix multiply (with perhaps an infinite number of dimensions).

Solution

The solution presented here is limited to presenting a matrix representation of the operator $d/dx$.

First, let us consider the finite case. Let $x$ be the independent variable with $n$ components and let the components of $x$ be defined such that $x_{m+1}=x_m+\mathrm{\Delta }x$ for all $m<n$ and for some constant $\mathrm{\Delta }x$. Also let $y=f(x)$. We wish to find the slope of the function at $y(x_m)$ for any $m$. To do this for the finite case, we will approximate the slope at a point $y(x_m)$ as being the slope of the line between the two points $y(x_{m-1})$ and $y(x_{m+1})$ given that $1<m<n$. For the case when $m=1$ or $m=n$, we approximate $dy/dx$ as the slope the lines between $y(x_1)$ and $y(x_n)$ respectively. These approximations are accomplished by the following matrix:

$\frac{d}{dx}=\frac{1}{2(\mathrm{\Delta }x)}\left[\begin{array}{ccccccccc}-2& 2& 0& 0& & & & & \\ -1& 0& 1& 0& & & \cdots & & \\ 0& -1& 0& 1& & & & & \\ \\ & & & & \ddots & & & & \\ \\ & ⋮& & & & -1& 0& 1& 0\\ & & & & & 0& -1& 0& 1\\ & & & & & 0& 0& -2& 2\end{array}\right]$

Note that we need to divide by $1/2(\mathrm{\Delta }x)$ because the distance between $x_{m-1}$ and $x_{m+1}$ is $2\mathrm{\Delta }x$. Similarly, the nonzero entries in the first and last rows are 2 to cancel out the 2 in the denominator. Using this matrix, we find that

$\left(\frac{d}{dx}\right)y=\frac{1}{2(\mathrm{\Delta }x)}\left[\begin{array}{ccccccccc}-2& 2& 0& 0& & & & & \\ -1& 0& 1& 0& & & \cdots & & \\ 0& -1& 0& 1& & & & & \\ \\ & & & & \ddots & & & & \\ \\ & ⋮& & & & -1& 0& 1& 0\\ & & & & & 0& -1& 0& 1\\ & & & & & 0& 0& -2& 2\end{array}\right]\left[\begin{array}{c}y(x_1)\\ y(x_2)\\ y(x_3)\\ \\ ⋮\\ \\ y(x_{n-2})\\ y(x_{n-1})\\ y(x_n)\end{array}\right]=\left[\begin{array}{c}[y(x_2)-y(x_1)]/\mathrm{\Delta }x\\ [y(x_3)-y(x_1)]/2(\mathrm{\Delta }x)\\ [y(x_4)-y(x_2)]/2(\mathrm{\Delta }x)\\ \\ ⋮\\ \\ [y(x_{n-1})-y(x_{n-3})]/2(\mathrm{\Delta }x)\\ [y(x_n)-y(x_{n-2})]/2(\mathrm{\Delta }x)\\ [y(x_n)-y(x_{n-1})]/\mathrm{\Delta }x\end{array}\right]$

which corresponds with the slopes we wished to obtain.

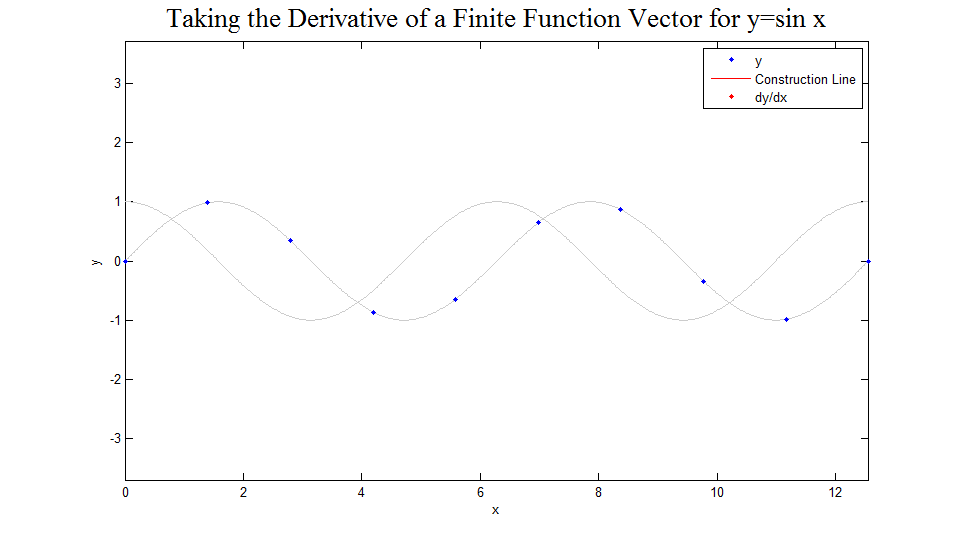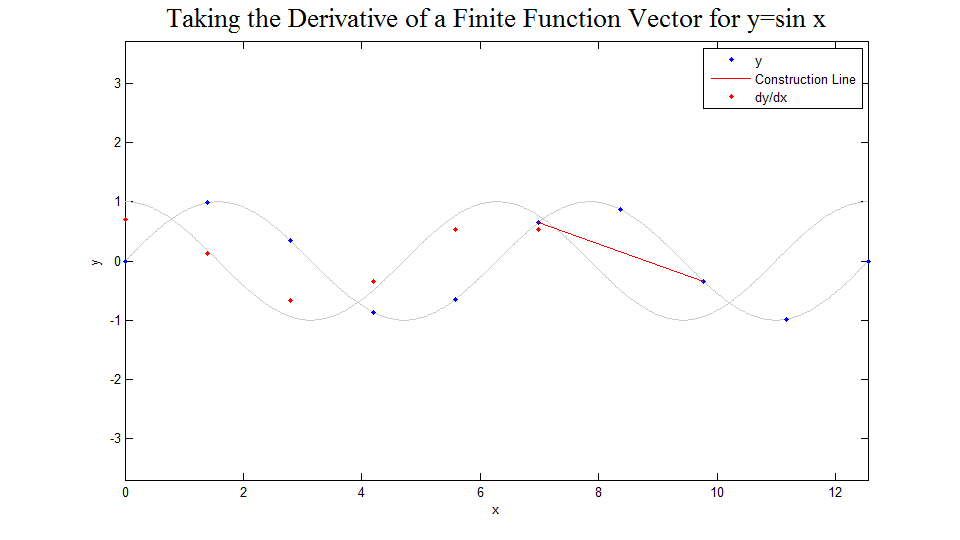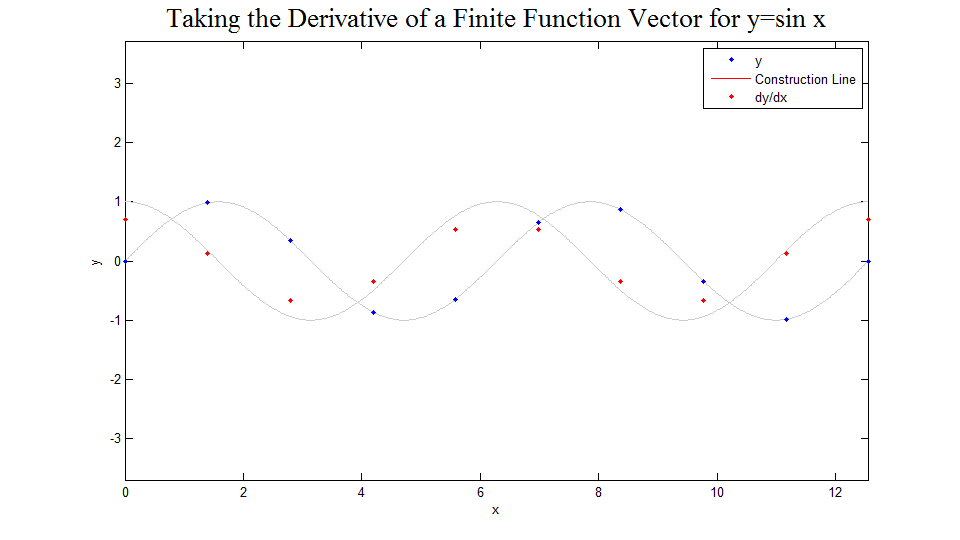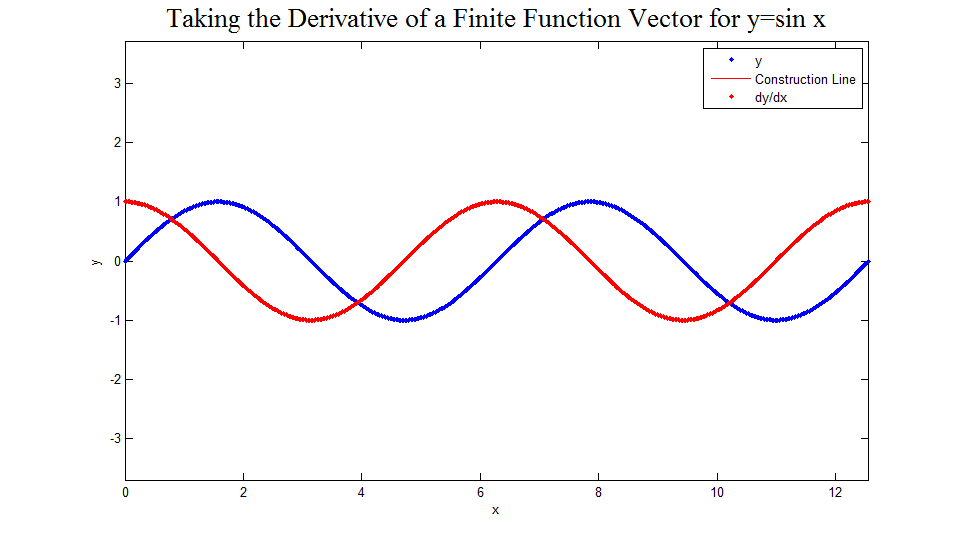
Solution Picture

The figure below was created to demonstrate how the above matrix works. First, 10 points of the function are displayed. Then for each point the line between the two adjacent points is drawn and the slope of that line is shown to be $dy/dx$ for the original point, calculated using the matrix shown above. After this has been done in the case of 10 points, the function and derivative vectors are shown for 15, 20, 30, 50, 100, 200, and 500 points. One can easily imagine the limiting case. The code used to develop this image can be found here.