HW7

Problem Statement
Figure out what happens if your sampled signal, $x(t)\!$, has frequency components only for ${\frac {f_{s}}{2}}<f<f_{s}\!$. Can you recover the original signal from it? If so, find the expression for $x(t)\!$ in terms of $x(nT)\!$.

Solution
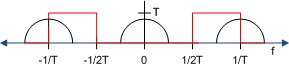
For ${\frac {f_{s}}{2}}<f<f_{s}\!$, our sampled signal $x(t)\!$ transformed to $X(f)\!$, is going to look like this. (Note: images not to scale.)

After sampling with frequency $f_{s}\!$, the signal is going to be shifted over by ${\frac {1}{T}}\!$, since $f_{s}={\frac {1}{T}}\!$. Our frequency now has the response,:br>

To recover the original signal $x(t)\!$, we will need a bandpass filter to filter out undesired frequency components, as indicated by the red line in the figure below.

We now have our original signal once again.

Now we need to find the equation for our filter. Then using the filter we can solve for x(t) since we will have our basis vectors.

The transfer function of the bandpass filter that will accomplish this for us is

$H(f)={\begin{cases}T,&{\mbox{ }}{\frac {1}{2T}}<|f|<{\frac {1}{T}}\\0,&{\mbox{ else }}\end{cases}}\!$

To find the expression for $h(t)\!$, the bandpass filter in the time domain, we can take the inverse Fourier transform.

$H(f)\!$.

$h(t)={\mathcal {F}}^{-1}[H(f)]={\frac {T}{j2}}{\Bigg [}{\frac {e^{j2\pi t/T}-e^{-j2\pi t/T}}{\pi t}}{\Bigg ]}-\ {\frac {T}{j2}}{\Bigg [}{\frac {e^{j\pi t/T}-e^{-j\pi t/T}}{\pi t}}{\Bigg ]}\!$

Recall Eulers identity pertaining to sin: $sin(\theta )={\frac {1}{j2}}(e^{j\theta }-e^{-j\theta })\!$, so

$h(t)={\frac {T}{j2}}{\Bigg [}{\frac {e^{j2\pi t/T}-e^{-j2\pi t/T}}{\pi t}}{\Bigg ]}-\ {\frac {T}{j2}}{\Bigg [}{\frac {e^{j\pi t/T}-e^{-j\pi t/T}}{\pi t}}{\Bigg ]}={\frac {2sin{\Big (}{\frac {2\pi t}{T}}{\Big )}}{\frac {2\pi t}{T}}}\ -\ {\frac {sin{\Big (}{\frac {\pi t}{T}}{\Big )}}{\frac {\pi t}{T}}}\!$

To simplyfy we can use sinc. $sinc(\theta )={\frac {sin(\pi \theta )}{\pi \theta }}\!$, so

$h(t)={\frac {2sin{\Big (}{\frac {2\pi t}{T}}{\Big )}}{\frac {2\pi t}{T}}}\ -\ {\frac {sin{\Big (}{\frac {\pi t}{T}}{\Big )}}{\frac {\pi t}{T}}}=2sinc{\Bigg (}{\frac {2t}{T}}{\Bigg )}-sinc{\Bigg (}{\frac {t}{T}}{\Bigg )}\!$

Now that we know $h(t)\!$, we can find $x(t)\!$ if we convolve the function for $x(t)\!$. Because we know that multiplication in one domain is equal if we convolve in the other domain.

after sampling with $h(t)\!$.

$x(t)=\sum _{n=-\infty }^{\infty }x(nT)\delta (t-nT)*{\Bigg [}2sinc{\Bigg (}{\frac {2t}{T}}{\Bigg )}-sinc{\Bigg (}{\frac {t}{T}}{\Bigg )}{\Bigg ]}$

$=\sum _{n=-\infty }^{\infty }x(nT){\Bigg [}2sinc{\Bigg (}{\frac {2(t-nT)}{T}}{\Bigg )}\ -\ sinc{\Bigg (}{\frac {t-nT}{T}}{\Bigg )}{\Bigg ]}\!$

(Pictures borrowed from Max's page)