How a CD player works - HW8

Max Woesner

Back to my Home Page

Homework #8 - How a CD player works

This page describes how a CD player works with no oversampling but with digital filtering, i.e. 1x oversampling.

When music for an audio CD is produced, the music has infinite data points and can be expressed as as a continuous function of time, or $x(t)\!$, such as the one shown below.

In the frequency domain, the signal $X(f)\!$ looks like this.

Since a CD has a finite amount of storage space, it would be impossible to store $x(t)\!$ on a CD. To solve this problem, the data is sampled at periodic intervals, creating a discrete function of time $x(nT)\!$, where $n\!$ is and integer and $T\!$ is the period between samples.
The sample rate $f_{s}={\frac {1}{T}}\!$. Aliasing can occur when you don't sample a signal fast enough to be able to reconstruct it accurately after sampling. To make sure this doesn't happen, we must follow Nyquist's theorem, which states that we must sample at a rate at least twice the fastest frequency of the signal we are sampling. Since human hearing can typically range from 20 Hz to 22 kHz, we want to sample at a rate greater than twice the highest frequency, or 44 kHz.
The discrete function of time $x(nT)\!$ can be expressed mathematically as $\sum _{n=-\infty }^{\infty }x(nT)\delta (t-nT)\!$. It might look like this.

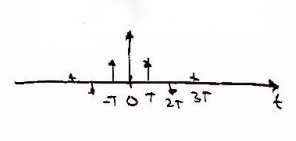
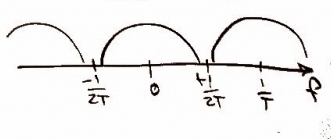
In the frequency domain, the function can be expressed either as ${\frac {1}{T}}\sum _{n=-\infty }^{\infty }X{\bigg (}f-{\frac {n}{T}}{\bigg )}$ or $\sum _{n=-\infty }^{\infty }x(nT)e^{-j2\pi fnT}\!$ and would look like this.

Oversampling can be used to create a smoother discrete function by filling in the gaps with more data points. For example, 8x oversampling, which is fairly common, would decrease the sampling period by a factor of eight, giving us a more accurate function of the original signal. For this page, however, we will focus on 1x oversampling. While no additional data points are added with 1x oversampling, the same process can be used as with 2x, 4x, or 8x oversampling by running the signal through a digital filter.

To do this, we want to convolve our discrete function by a standard finite impulse response (FIR) filter we will call $h(t)\!$.

$h(t)\!$ can be defined as $h(t)=\sum _{m=-M}^{M}h{\bigg (}{\frac {mT}{n'}}{\bigg )}\,\delta {\bigg (}{\frac {t-mT}{n'}}{\bigg )}\!$, where $n'\!$ is the oversampling rate.
In this case, $n'=1\!$, so

$h(t)=\sum _{m=-M}^{M}h(mT)\,\delta (t-mT)\!$

. Since we are using 1x oversampling, the function won't look any different than the original discrete function.

The frequency response of this is $H(f)={\mathcal {F}}{\Bigg [}\sum _{m=-M}^{M}h(mT)\,\delta (t-mT){\Bigg ]}=\sum _{m=-M}^{M}h(mT)e^{-j2\pi fmT}$, which looks like this.

The convolution of our discrete function and $h(t)\!$ can be expressed mathematically as
$x(t)*h(t)\ =\sum _{n=-\infty }^{\infty }x(nT)\delta (t-nT)*\sum _{m=-M}^{M}h(mT)\,\delta (t-mT)\!$

$=\sum _{n=-\infty }^{\infty }x(nT)\sum _{m=-M}^{M}h(mT)\,\delta (t-mT-nT)\!$

Let $l=m+n\!$, so $n=l-m\!$, and

$x(t)*h(t)\ =\sum _{n=-\infty }^{\infty }\sum _{m=-M}^{M}x[(l-m)T]h(mT)\,\delta (t-lT)\!$

Let us define $\sum _{m=-M}^{M}x[(l-m)T]h(mT)\!$ as the function $y(lT)\!$, so

$x(t)*h(t)\ =\sum _{l=-\infty }^{\infty }y(lT)\delta (t-lT)\!$. It would look something like this.

Note that $y(lT)\!$ is both a discrete convolution sum and a matrix multiply.

The frequency equivalent would be $\sum _{l=-\infty }^{\infty }y(lT)e^{-j2\pi flT}\!$. It can also be expressed as
${\frac {1}{T}}\sum _{n=-\infty }^{\infty }X{\bigg (}f-{\frac {n}{T}}{\bigg )}\cdot H(f)$, or $\ {\frac {1}{T}}\sum _{n=-\infty }^{\infty }X{\bigg (}f-{\frac {n}{T}}{\bigg )}\cdot \sum _{m=-M}^{M}h(mT)e^{-j2\pi fmT}\!$

This is what it would look like.


This pre-emphasis exaggerates the high frequencies so that when the signal goes through the D/A converter and the low pass filter, both of which de-emphasize the high frequencies, the signal coming out will be close to the original signal.
Now we are ready to convolve our function with a pulse function $p(t)\!$, which is done by the D/A converter in a CD player.

$p(t)=u{\bigg (}t+{\frac {T}{2}}{\bigg )}-u{\bigg (}t-{\frac {T}{2}}{\bigg )}\!$ and would look like this



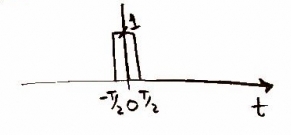
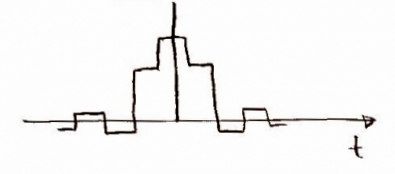
The convolution looks like this: $\sum _{l=-\infty }^{\infty }y(lT)\delta (t-lT)*p(t)=\sum _{l=-\infty }^{\infty }y(lT)p(t-lT)\!$

This convolution gives us a step function, such as the one below.

The frequency equivalent of $p(t)\!$, or $P(f)\!$, can be expressed as $P(f)=Tsinc(fT)\!$ and will look something like this.


Since the equivalent to convolution in time is multiplication in frequency, we will multiply $P(f)\!$ by $\sum _{n=-\infty }^{\infty }x(nT)e^{-j2\pi fnT}\!$, or
$Tsinc(fT)\cdot \sum _{n=-\infty }^{\infty }x(nT)e^{-j2\pi fnT}\!$. It would look like this.


Now we can simply run the signal through a low pass filter and send it to the speakers for playback.
In the time domain, an RC low pass filter, $g(t)\!$, might look like this.


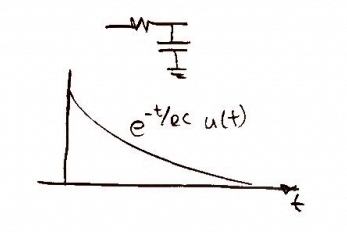
In time, we want to convolve our function with the low pass filter, or $\sum _{l=-\infty }^{\infty }y(lT)p(t-lT)*g(t)\!$

The frequency response of the lowpass filter, $G(f)\!$, would look something like this.


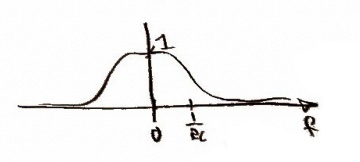
In frequency, we would want to multiply our function with the low pass filter, or $Tsinc(fT)\cdot \sum _{n=-\infty }^{\infty }x(nT)e^{-j2\pi fnT}\cdot G(f)\!$

And that is probably more than you ever wanted to know about how a CD player works.