FIRJEW: Difference between revisions
Jump to navigation
Jump to search
| (6 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
==Finite Impulse Response Filters== | ==Finite Impulse Response Filters== | ||
A Finite Impurse Response filter (aka FIR filter) is a type of filter often used in digital signal processing and has no feedback | A Finite Impurse Response filter (aka FIR filter) is a type of filter often used in digital signal processing and has no feedback loop. Because there is no feedback, the response of an FIR filter to an impulse is finite. | ||
The equation for an FIR filter would look like the following: | |||
<small>Principle author: Jeffrey Wonoprabowo</small> | <center><math>h(mT) = T \int_{-v}^v \hat H (f) e^{j 2 \pi f m t} df </math></center> | ||
where the desired frequencies are in the range from <math>-v</math> to <math>v</math> and <math> \hat H (f) </math> is the desired response. | |||
Example: Desing an FIR low pass filter to pass between <math> - \frac{1}{4T} < f < \frac{1}{4T} </math> and reject the rest. | |||
<math>\hat H (f) = \begin{cases} 1, & |f| \le \frac{1}{4T} \\ 0, & else \end{cases} </math> | |||
The FIR filter would then be: | |||
<math> h(mT) = T \int_{\frac{-1}{4T}}^{\frac{1}{4T}} 1 e^{j 2 \pi f m t} df = T\frac{e^{j 2 \pi \frac{1}{4T} m T} - e^{j 2 \pi \frac{-1}{4T} m T}}{j 2 \pi m T}</math> | |||
<math> = \frac{e^{j 2 \pi \frac{1}{4T} m T} - e^{j 2 \pi \frac{-1}{4T} m T}}{j 2 \pi m} = \left ( \frac{1}{2} \right) \frac{sin \left ( \frac{\pi m}{2} \right)} {\left(\frac{\pi m}{2}\right)}</math> | |||
and the actual frequency response would then be: | |||
<math>\sum_{m=-M}^M h(mT) e^{- j 2 \pi f m T} = \sum_{m=-M}^M \frac{ sin \left ( \frac{\pi m}{2} \right) }{\pi m} e^{- j 2 \pi f m T} </math> | |||
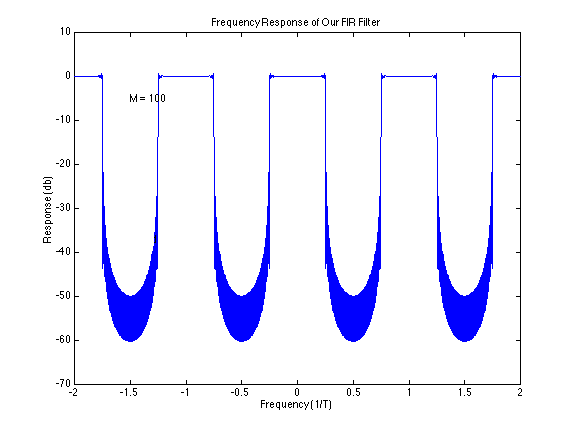
The frequency response plot of this particular FIR filter would look like this: | |||
[[Image:Frequency_Response_Pict.png]] | |||
==Related Pages== | |||
[[AdaptiveFIRJEW | Adaptive FIR Filters]] | |||
<small>Principle author: Jeffrey Wonoprabowo | |||
Image of the frequency response plot taken from the FIR example page [[FIR_Filter_Example|here]]. | |||
</small> | |||
Latest revision as of 01:24, 13 December 2005
Finite Impulse Response Filters
A Finite Impurse Response filter (aka FIR filter) is a type of filter often used in digital signal processing and has no feedback loop. Because there is no feedback, the response of an FIR filter to an impulse is finite.
The equation for an FIR filter would look like the following:
where the desired frequencies are in the range from to and is the desired response.
Example: Desing an FIR low pass filter to pass between and reject the rest.
The FIR filter would then be:
and the actual frequency response would then be:
The frequency response plot of this particular FIR filter would look like this:
Related Pages
Principle author: Jeffrey Wonoprabowo
Image of the frequency response plot taken from the FIR example page here.