ASN10 - Quadrature sampling demonstration: Difference between revisions
Jump to navigation
Jump to search
Jodi.Hodge (talk | contribs) No edit summary |
Jodi.Hodge (talk | contribs) No edit summary |
||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[Jodi Hodge|Back to my home page]] |
[[Jodi Hodge|Back to my home page]] |
||
Assignment was actually done in class by professor. |
Assignment was actually done in class by professor. Classmate [[Max Woesner ]] has posted the Octave code and plot. |
||
In Octave we were to plot |
|||
[http://www.example.com link title] |
|||
| ⚫ | |||
<br><b>Problem Statement</b><br><br> |
|||
| ⚫ | |||
<b>Solution</b><br> |
|||
While we can't sum to infinity in the computer, we can get a close approximation summing over a large enough range of <math> n \!</math><br> |
|||
I found summing over <math> n = 1:1000 \!</math> was about the most the computer could handle reasonably.<br> |
|||
The following script was written in MATLAB to produce the desired plot. <br> |
|||
<pre> |
<pre> |
||
clear all; |
clear all; |
||
| Line 33: | Line 28: | ||
ylabel('Sampling Waveform') |
ylabel('Sampling Waveform') |
||
</pre><br> |
</pre><br> |
||
Running the MATLAB script above gives us the following plot.<br> |
|||
[[Image:Quadrature sampling.jpg]]<br> |
[[Image:Quadrature sampling.jpg]]<br> |
||
Latest revision as of 17:20, 18 December 2009
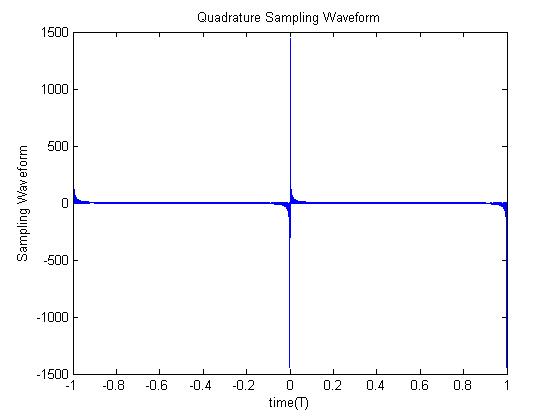
Assignment was actually done in class by professor. Classmate Max Woesner has posted the Octave code and plot.
In Octave we were to plot
clear all;
close all;
sum = 0;
T = 1;
t = -T:0.0001:T;
N = 1000;
for n = 1:N;
if n==0
h = 0;
else
h = 2/T;
end
sum = sum+h*sin(2*pi*n*t/T);
end
plot(t,sum)
title('Quadrature Sampling Waveform')
xlabel('time(T)')
ylabel('Sampling Waveform')
