CDPlayerJEW: Difference between revisions
| Line 19: | Line 19: | ||
<center><math>p(t) = u(t+\frac{T}{2}) - u(t-\frac{T}{2})</math></center> | <center><math>p(t) = u(t+\frac{T}{2}) - u(t-\frac{T}{2})</math></center> | ||
<center><math>\sum_{n=-\infty}^\infty x(nT) \delta (t-nT) * p(t) = \sum_{n=-\infty}^\infty x(nT)p(t-nT) </math></center> | |||
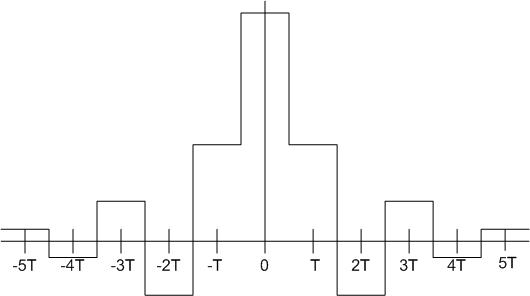
This convolution, which is the convolution of the discretized signal and <math>p(t)</math>, a pulse function, will yield a graph that is no longer discrete, but is stepped. The following is an example: | |||
<center>[[Image:DAOutput.jpg|Convolved Graph]]</center> | |||
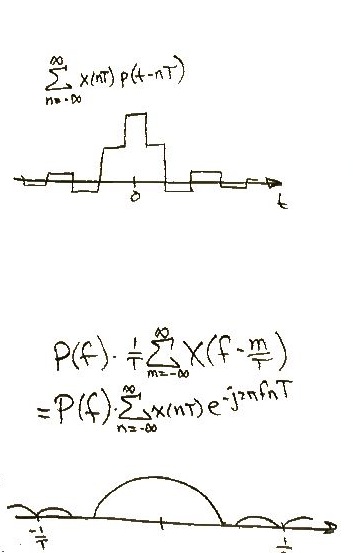
In the frequency domain, the above stepped signal will look like the following: | |||
<center>[[Image:TnD.jpg|Convolution (Time Domain) and it's frequency domain counterpart]]</center> | |||
<small>- Principle author of this page: Jeffrey Wonoprabowo | <small>- Principle author of this page: Jeffrey Wonoprabowo | ||
- Image Player Diagram by Aric Goe or Todd Caswell (not sure which since both of them had it on their pages)</small> | - Image of CD Player Diagram and Convolution by Aric Goe or Todd Caswell (not sure which since both of them had it on their pages)</small> | ||
Revision as of 15:57, 5 December 2005
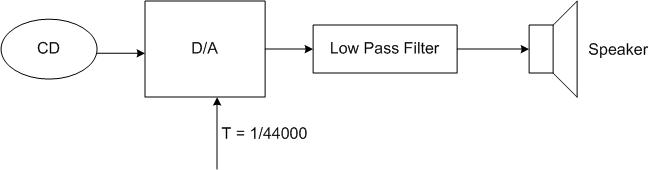
How a CD Player Works
A CD player reads a dicrete set of data off a CD. In short, a CD player takes this data and sends it through a digitla to analog converter, then through a low pass filter, and finally is output through speakers. A simple diagram illustrates this below.
When an audio CD is recorded, the music has an infinite amount of data points and can be represented as a continuous function of time . Because a medium, such as a CD, has a finite amount of space, it will not be able to hold since it has an infinite amount of data. Instead, the music is sampled at intervals to create a discrete function of time where is an integer and is the interval between samples.
This discrete signal can be represented mathematically by:
Then, the discrete signal is convolved by the D/A converter with a function :
This convolution, which is the convolution of the discretized signal and , a pulse function, will yield a graph that is no longer discrete, but is stepped. The following is an example:
In the frequency domain, the above stepped signal will look like the following:
- Principle author of this page: Jeffrey Wonoprabowo
- Image of CD Player Diagram and Convolution by Aric Goe or Todd Caswell (not sure which since both of them had it on their pages)