ASN10 - Quadrature sampling demonstration: Difference between revisions
Jump to navigation
Jump to search
Jodi.Hodge (talk | contribs) No edit summary |
Jodi.Hodge (talk | contribs) No edit summary |
||
| Line 3: | Line 3: | ||
Assignment was actually done in class by professor. | Assignment was actually done in class by professor. | ||
In Octave we were to plot <math> \ \frac{2}{T} \sum_{n=1}^\infty sin\bigg(\frac{2 \pi nt}{T}\bigg) \!</math><br><br> | |||
Classmate [[Max Woesner ]] has also demonstrated it as shown below with similar code. | |||
<pre> | <pre> | ||
clear all; | clear all; | ||
| Line 33: | Line 27: | ||
ylabel('Sampling Waveform') | ylabel('Sampling Waveform') | ||
</pre><br> | </pre><br> | ||
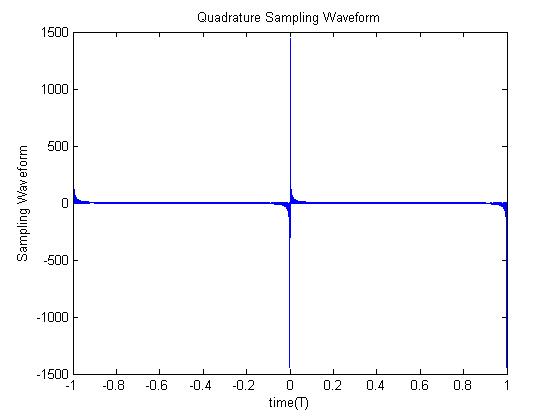
The MATLAB script gives <br> | |||
[[Image:Quadrature sampling.jpg]]<br> | [[Image:Quadrature sampling.jpg]]<br> | ||
Revision as of 11:18, 3 December 2009
Assignment was actually done in class by professor.
In Octave we were to plot
Classmate Max Woesner has also demonstrated it as shown below with similar code.
clear all;
close all;
sum = 0;
T = 1;
t = -T:0.0001:T;
N = 1000;
for n = 1:N;
if n==0
h = 0;
else
h = 2/T;
end
sum = sum+h*sin(2*pi*n*t/T);
end
plot(t,sum)
title('Quadrature Sampling Waveform')
xlabel('time(T)')
ylabel('Sampling Waveform')
The MATLAB script gives