Fall 2009/JonathanS

Problem

A simple pendulum with a length L = 0.5m is pulled back and released from an initial angle ${\theta }_0=12^o$. Then it is run with a forcing function of cos(3$\theta$) Find an equation that gives the angle of the pendulum at any given time t.

Solution

Assuming no damping and a small angle($\theta <15^o$), the equation for the motion of a simple pendulum can be written as

$\frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}+\frac{g}{\ell }\theta =cos(3\theta ).$

Substituting values we get

$\frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}+\frac{9.81}{0.5}\theta =cos(3\theta ).$

$\Rightarrow \frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}+19.62\theta =cos(3\theta ).$

Remember the identities

${ℒ}\{f(t)\}=F(s)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{e}^{-st}f(t)dt.$

${ℒ}\{f^{{\text{'}}^{\prime }}(t)\}=s^{2}F(s)-sf(0)-f^{\text{'}}(0)$

Now we can take the Laplace Transform to change the second order differential equation, from the t domain, into a simple linear equation, from the s domain, that's much easier to work with

${ℒ}\{\frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}+19.62\theta \}=s^{2}F(s)-sf(0)-f^{\text{'}}(0)+19.62\theta ={ℒ}\{cos(3\theta )\}$

$\Rightarrow$ $s^2\mathit{\theta }-s\theta (0)-{\theta }^{\text{'}}(0)+19.62\mathit{\theta }=\frac{s}{s^2+9}$

Since we know that $\theta (0)=12^o$ and the initial velocity ${\theta }^{\text{'}}(0)=0$ we get

$s^2\mathit{\theta }-12s+19.62\mathit{\theta }=\frac{s}{s^2+9}$

$\Rightarrow$ $\mathit{\theta }(s^2+19.62)=\frac{s}{s^2+9}+12s$

$\Rightarrow$ $\mathit{\theta }(s^2+19.62)=\frac{s}{s^2+9}+\frac{12s(s^2+9)}{s^2+9}$

$\Rightarrow$ $\mathit{\theta }(s^2+19.62)=\frac{(12s^3+109s)}{s^2+9}$

$\Rightarrow$ $\mathit{\theta }=\frac{(12s^3+109s)}{(s^2+9)(s^2+19.62)}$

$\Rightarrow$ $\mathit{\theta }=\frac{12s^3+109s}{(s^4+28.62s^2+176.58)}$

Now we can take the inverse Laplace Transform to convert our equation back into the time domain

${{ℒ}}^{-1}\left\{\frac{12s^3+109s}{(s^4+28.62s^2+176.58)}\right\}=0.094162cos(3t)+11.9058cos(4.42945t)$

This will give us the angle (in degrees) of the pendulum at any given time t.

Initial Value Theorem

We can use the Initial Value Theorem as a check that our initial values for the problem are valid.

${ℒ}\{f^{\text{'}}(t)\}=sF(s)-f(0^{-})=\underset{0^{-}}{\overset{\mathrm{\infty }}{\int }}{f}^{\text{'}}(t)e^{-st}dt$

$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{\lim }{ℒ}\{f^{\text{'}}(t)\}& =\underset{n\to \mathrm{\infty }}{\lim }sF(s)-f(0^{-})\\ & =\underset{n\to \mathrm{\infty }}{\lim }sF(s)-f(0^{-})=0\\ & =\underset{n\to \mathrm{\infty }}{\lim }sF(s)=f(0^{-})\\ \end{array}$

Below we will use this theorem to check the values for our problem.

$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{\lim }{ℒ}\{f^{\text{'}}(t)\}& =\underset{n\to \mathrm{\infty }}{\lim }sF(s)-f(0^{-})=\underset{n\to \mathrm{\infty }}{\lim }\underset{0^{-}}{\overset{\mathrm{\infty }}{\int }}{f}^{\text{'}}(t)e^{-st}dt\\ & =\underset{n\to \mathrm{\infty }}{\lim }s\left(\frac{12s^3+109s}{(s^4+28.62s^2+176.58)}\right)-f(0^{-})=0\\ & =\underset{n\to \mathrm{\infty }}{\lim }s\left(\frac{12s^3+109s}{(s^4+28.62s^2+176.58)}\right)=f(0^{-})\\ 12& =f(0^{-})\\ \end{array}$

This value $f(0^{-})=12$ is the initial angle we gave the pendulum so it checks out.

Final Value Theorem

We can use the Final Value Theorem as a check that our final values for the problem are valid.

${ℒ}\{f^{\text{'}}(t)\}=sF(s)-f(\mathrm{\infty })=\underset{0^{-}}{\overset{\mathrm{\infty }}{\int }}{f}^{\text{'}}(t)e^{-st}dt$

$\begin{array}{rl}\underset{n\to 0}{\lim }{ℒ}\{f^{\text{'}}(t)\}& =\underset{n\to 0}{\lim }sF(s)-f(\mathrm{\infty })\\ & =\underset{n\to 0}{\lim }sF(s)-f(\mathrm{\infty })=0\\ & =\underset{n\to 0}{\lim }sF(s)=f(\mathrm{\infty })\\ \end{array}$

Below we will use this theorem to check the values for our problem.

$\begin{array}{rl}\underset{n\to 0}{\lim }{ℒ}\{f^{\text{'}}(t)\}& =\underset{n\to 0}{\lim }sF(s)-f(\mathrm{\infty })=\underset{n\to 0}{\lim }\underset{0^{-}}{\overset{\mathrm{\infty }}{\int }}{f}^{\text{'}}(t)e^{-st}dt\\ & =\underset{n\to 0}{\lim }s\left(\frac{12s^3+109s}{(s^4+28.62s^2+176.58)}\right)-f(\mathrm{\infty })=0\\ & =\underset{n\to 0}{\lim }s\left(\frac{12s^3+109s}{(s^4+28.62s^2+176.58)}\right)=f(\mathrm{\infty })\\ 0& =f(\mathrm{\infty })\\ \end{array}$

This is zero because the average angle as time goes to infinity will be zero (halfway between -12 and 12 degrees).

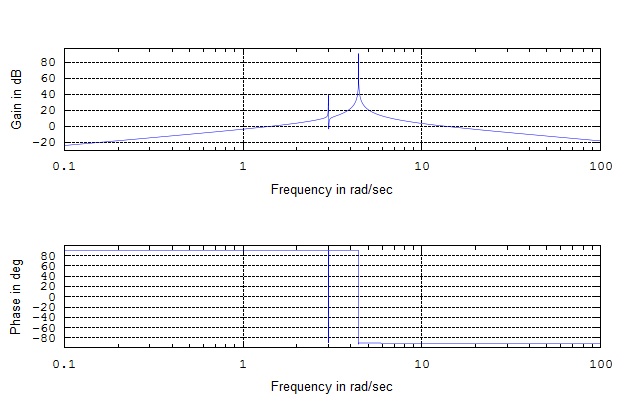
Bode Plots

To find the bode plot we use the function

$H(s)=\frac{12s^3+109s}{(s^4+28.62s^2+176.58)}$

Entering this into a program such as Maple, Octave, or MATLAB will give you a plot that looks like this

Asymptotes & Break Points

In this section I will describe how you can use the transfer function to quickly estimate what the bode plot will look like.

In this case our transfer function is

Convolution

Now we will use convolution to find the output of our of our system.