A octave/MATLAB script to show how Nyquist's formula

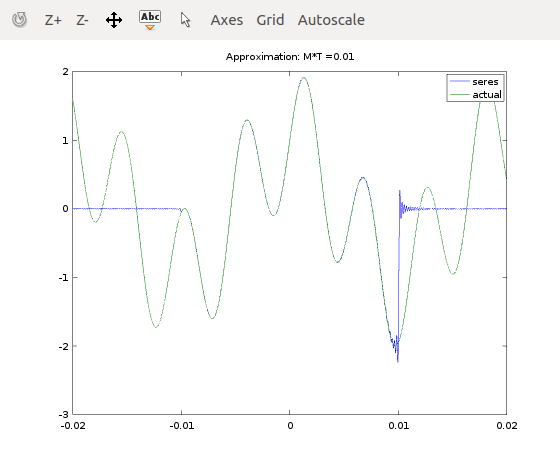
Nyquist showed that if the function $x(t)$ was band limited to less than $1 \over {2T}$ Hz, then it could be represented by $x(t)=\sum _{k=-\infty }^{\infty }x(kT)sinc((t-kT)/T)$. This octave script plots this for finite values of $M$ in the sum, $x(t)=\sum _{k=-M}^{M}x(kT)sinc((t-kT)/T)$.

% This is a script to check Nyquist's formula giving a low pass
% function as a function of its sample points, x(kT).
% Note that the approximation is pretty good for -M*T<t<M*T.
M=100; % Number of terms 
T=1e-4;
Tf=.02;

function x0 = x(t0)
x0=sin(2*pi*180*t0)+cos(2*pi*50*t0);
endfunction
t=-Tf:T/1000:Tf;
x1=zeros(size(t));
for k=-M:M
  x1 = x1 + x(k*T).*sinc((t-k*T)/T);
end
plot(t,x1,t,x(t))
title(strcat('Approximation: M*T =',num2str(M*T)))
legend('seres','actual')