Fall 2009/JonathanS

Problem

A simple pendulum with a length L = 0.5m is pulled back and released from an initial angle ${\theta }_0=12^o$. Then it is run with a forcing function of cos(3$\theta$) Find an equation that gives the angle of the pendulum at any given time t.

Solution

Assuming no damping and a small angle($\theta <15^o$), the equation for the motion of a simple pendulum can be written as

$\frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}+\frac{g}{\ell }\theta =cos(3\theta ).$

Substituting values we get

$\frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}+\frac{9.81}{0.5}\theta =cos(3\theta ).$

$\Rightarrow \frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}+19.62\theta =cos(3\theta ).$

Remember the identities

${ℒ}\{f(t)\}=F(s)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{e}^{-st}f(t)dt.$

${ℒ}\{f^{{\text{'}}^{\prime }}(t)\}=s^{2}F(s)-sf(0)-f^{\text{'}}(0)$

Now we can take the Laplace Transform to change the second order differential equation, from the t domain, into a simple linear equation, from the s domain, that's much easier to work with

${ℒ}\{\frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}+19.62\theta \}=s^{2}F(s)-sf(0)-f^{\text{'}}(0)+19.62\theta ={ℒ}\{cos(3\theta )\}$

$\Rightarrow$ $s^2\mathit{\theta }-s\theta (0)-{\theta }^{\text{'}}(0)+19.62\mathit{\theta }=\frac{s}{s^2+9}$

Since we know that $\theta (0)=12^o$ and the initial velocity ${\theta }^{\text{'}}(0)=0$ we get

$s^2\mathit{\theta }-12s+19.62\mathit{\theta }=\frac{s}{s^2+9}$

$\Rightarrow$ $\mathit{\theta }(s^2+19.62)=\frac{s}{s^2+9}+12s$

$\Rightarrow$ $\mathit{\theta }(s^2+19.62)=\frac{s}{s^2+9}+\frac{12s(s^2+9)}{s^2+9}$

$\Rightarrow$ $\mathit{\theta }(s^2+19.62)=\frac{(12s^3+109s)}{s^2+9}$

$\Rightarrow$ $\mathit{\theta }=\frac{(12s^3+109s)}{(s^2+9)(s^2+19.62)}$

$\Rightarrow$ $\mathit{\theta }=\frac{12s^3+109s}{(s^4+28.62s^2+176.58)}$

Now we can take the inverse Laplace Transform to convert our equation back into the time domain

${{ℒ}}^{-1}\left\{\frac{12s^3+109s}{(s^4+28.62s^2+176.58)}\right\}=0.094162cos(3t)+11.9058cos(4.42945t)$

This will give us the angle (in degrees) of the pendulum at any given time t.

Initial Value Theorem

We can use the Initial Value Theorem as a check that our initial values for the problem are valid.

${ℒ}\{f^{\text{'}}(t)\}=sF(s)-f(0^{-})=\underset{0^{-}}{\overset{\mathrm{\infty }}{\int }}{f}^{\text{'}}(t)e^{-st}dt$

$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{\lim }{ℒ}\{f^{\text{'}}(t)\}& =\underset{n\to \mathrm{\infty }}{\lim }sF(s)-f(0^{-})\\ & =\underset{n\to \mathrm{\infty }}{\lim }sF(s)-f(0^{-})=0\\ & =\underset{n\to \mathrm{\infty }}{\lim }sF(s)=f(0^{-})\\ \end{array}$

Below we will use this theorem to check the values for our problem.

$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{\lim }{ℒ}\{f^{\text{'}}(t)\}& =\underset{n\to \mathrm{\infty }}{\lim }sF(s)-f(0^{-})=\underset{n\to \mathrm{\infty }}{\lim }\underset{0^{-}}{\overset{\mathrm{\infty }}{\int }}{f}^{\text{'}}(t)e^{-st}dt\\ & =\underset{n\to \mathrm{\infty }}{\lim }s\left(\frac{12s^3+109s}{(s^4+28.62s^2+176.58)}\right)-f(0^{-})=0\\ & =\underset{n\to \mathrm{\infty }}{\lim }s\left(\frac{12s^3+109s}{(s^4+28.62s^2+176.58)}\right)=f(0^{-})\\ 12& =f(0^{-})\\ \end{array}$

This value $f(0^{-})=12$ is the initial angle we gave the pendulum so it checks out.

Final Value Theorem

We can use the Final Value Theorem as a check that our final values for the problem are valid.

${ℒ}\{f^{\text{'}}(t)\}=sF(s)-f(\mathrm{\infty })=\underset{0^{-}}{\overset{\mathrm{\infty }}{\int }}{f}^{\text{'}}(t)e^{-st}dt$

$\begin{array}{rl}\underset{n\to 0}{\lim }{ℒ}\{f^{\text{'}}(t)\}& =\underset{n\to 0}{\lim }sF(s)-f(\mathrm{\infty })\\ & =\underset{n\to 0}{\lim }sF(s)-f(\mathrm{\infty })=0\\ & =\underset{n\to 0}{\lim }sF(s)=f(\mathrm{\infty })\\ \end{array}$

Below we will use this theorem to check the values for our problem.

$\begin{array}{rl}\underset{n\to 0}{\lim }{ℒ}\{f^{\text{'}}(t)\}& =\underset{n\to 0}{\lim }sF(s)-f(\mathrm{\infty })=\underset{n\to 0}{\lim }\underset{0^{-}}{\overset{\mathrm{\infty }}{\int }}{f}^{\text{'}}(t)e^{-st}dt\\ & =\underset{n\to 0}{\lim }s\left(\frac{12s^3+109s}{(s^4+28.62s^2+176.58)}\right)-f(\mathrm{\infty })=0\\ & =\underset{n\to 0}{\lim }s\left(\frac{12s^3+109s}{(s^4+28.62s^2+176.58)}\right)=f(\mathrm{\infty })\\ 0& =f(\mathrm{\infty })\\ \end{array}$

This is zero because the average angle as time goes to infinity will be zero (halfway between -12 and 12 degrees).

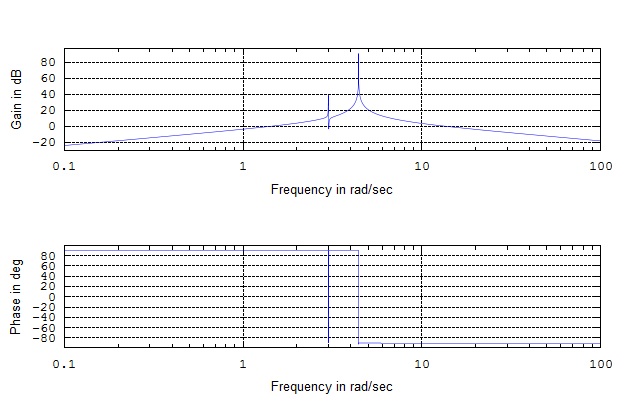
Bode Plot

To find the bode plot we use the function $H(s)=\frac{12s^3+109s}{(s^4+28.62s^2+176.58)}$

Entering this into a program such as Maple, Octave, or MATLAB will give you a plot that looks like this